Broadband plane wave with a constant oblique incident angle¶

Theoretical Background¶

Tidy3D provides two methods for simulating angled plane waves for periodic structures:

1. Fixed in-plane k vector mode, and
2. Fixed angle mode.

Both methods produce the same results at the central source frequency, but their behavior away from the central frequency differs significantly and it is important to understand the differences between the two approaches.

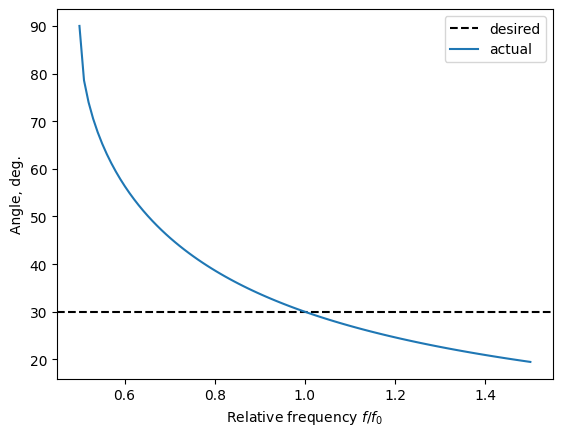
The first method is based on injecting an angled plane wave source and imposing the Bloch boundary conditions on periodic domain edges (see tutorial on boundary conditions for details). Fields that satisfy Bloch boundary conditions undergo a change of constant factor across periodic boundaries. For example, if a plane wave with frequency $f_0$ and angle $\theta_0$ with the $x$ axis is propagating along axis $z$, then the fields will differ by a factor of $\exp(-i \sin(\theta_0) f_0 L_x)$ between opposite edges in the $x$ direction. If we consider another plane wave with the same angle but a different frequency $f_1$, then this second plane wave would undergo a different phase difference of $\exp(-i \sin(\theta_0) f_1 L_x)$. However, the FDTD method performs evolution of time domain fields, which consist of a continuous spectrum of waves in a certain frequency range, and only single phase factor can be applied at periodic Bloch boundaries. Typically, this factor is selected to correspond to the central frequency of the injected plane wave, which means that only fields at the central frequency would satisfy the desired angle. Angles of frequency domain fields computed for wavelengths away from the central one will differ from $\theta_0$. By performing simple calculations it is easy to show that the field angle dependence on frequency is $\theta_{actual}(f) = \arcsin(\sin(\theta_0) \frac{f_0}{f})$.

A simple code below visualizes this dependence in case of $\theta_0 = 30$ deg.

The second approach avoids the issue of angular frequency dependency by modifying the governing Maxwell equations to include the correct phase difference for all frequencies. The resulting equations to be solved in fact represent propagation of normally incident plane wave but with additional coupling factors. These coupling terms increase the computational complexity, which leads to the following two disadvantages of the second approach compared to the first one.

1. Simulation cost¶

First of all, it increases the cost of running a simulation: the fixed angle technique could lead to a significant increase of simulation cost. This increase depends on the angle of propagation plane wave. For example, for a plane wave inclined at angle $\theta=5$ degrees the simulation cost increase compared to the fixed in-plane k simulation would be approximately a factor of 2, while for a plane wave angled at $\theta = 50$ degrees such an increase would be approximately a factor of 4. The user is encouraged to use web.estimate() cost estimation function before submitting simulation for running.

Despite increased simulation costs, the fixed angle technique can significantly outperform the fixed in plane k technique if many frequency points are of interest. For example, to accurately compute scattering and transmission of an oblique plane wave at a given angle of $\theta = 50$ deg. and at 100 frequency points using Bloch BC it would require creating a parameter sweep of the source central frequency. Essentially treating each simulation as a frequency domain simulation. Since tasks are run in parallel on Flexcompute servers, the speed might not actually be much worse but the cost linearly scales with the number of sampled frequency points. While using the fixed angle technique it would require only one simulation resulting, with the total cost reduced by a factor of [cost of running 100 Bloch BC simulations] / [cost of running 1 fixed angle simulation] = 100 / 4 = 25.

2. Stability¶

Another disadvantage of the fixed angle technique that couple from additional coupling terms, is more frequent divergence issues. In most cases this could be alleviated by either reducing the courant factor or switching absorbing boundary conditions in the propagation direction to adiabatic Absorber. Overall, the user should exercise more caution when dealing with fixed angle simulations.

Tidy3D Python API¶

Oblique incident plane waves can be defined in Tidy3D Python API using source types TFSF and PlaneWave. Currently, TFSF supports only the fixed in-plane k approach, while PlaneWave supports both. Switching between the two techniques for PlaneWave sources is simply accomplished by changing the field angular_spec from FixedInPlaneKSpec (default) to FixedAngleSpec. Additionally, for the fixed in plane k simulations Bloch boundary conditions must be correctly set up, while for the fixed angle simulations periodic boundary conditions are simply set to Periodic.

Demonstration: Transmission through a Dispersive Stack.¶

Let us know demonstrate the application of these two techniques. We will revisit the example of a plane wave transmission through a layered stack of dispersive materials. This example admits an analytical solution using the transfer matrix method, which makes it easy to benchmark the accuracy of both methods.

Simulation setup¶

Import Tidy3D and other packages.

Define angles of the injected plane wave.

Define the frequency range of interest.

We will consider a stack of 4 layers with thicknesses 0.5, 0.2, 0.4, and 0.3 $\mu m$.

Layers are made or dispersive and non-dispersive materials.

Given the defined layer thicknesses and material definition, programmatically create corresponding Tidy3D structures.

To analyze the simulation results we will record the total transmitted flux. Additionally, for visual comparison we will record the actual field distributions at three different frequency points: the central frequency of the source and the end points of the frequency range defined above.

As it was mentioned in the introduction, when setting up a fixed in-plane k simulation, one must select the corresponding angular_spec in a PlaneWave source definition, and set up compatible periodic Bloch boundary conditions.

Note that FixedInPlaneKSpec is the default value for field angular_spec. Thus, in the code below one can omit explicitly setting this field.

source from (default) to . Additionally, for the fixed in plane k simulations Bloch boundary conditions must be correctly set up, while for the fixed angle simulations periodic boundary conditions are simply set to Periodic.

When setting up a fixed angle simulation one needs to set angular_spec to FixedAngleSpec in the source definition, and apply simple periodic boundary conditions.

Define final specifications for both a fixed in-plane k simulation and a fixed angle one.

Running simulations¶

Before submitting the simulations to our servers for solving, let us compare the estimated simulation costs.

Thus, in this particular situation the fixed angle simulation would be approximately charged more by a factor of

Submit and run simulations as usual.

In addition, we will submit and run the exactly same simulation setups but with no structures included. This is done to obtain the precise amounts of power injected at all frequencies (recall that the injected power might slightly deviate from the intended value away from the central frequency due to numerical discretizations).

Simulation results analysis¶

We start analysis of simulation resutls with a visual inspection of field distributions recorded at three different frequencies. In the code below we plot the fixed in-plane k simulation results in the top row and the fixed angle simulation results in the second row.

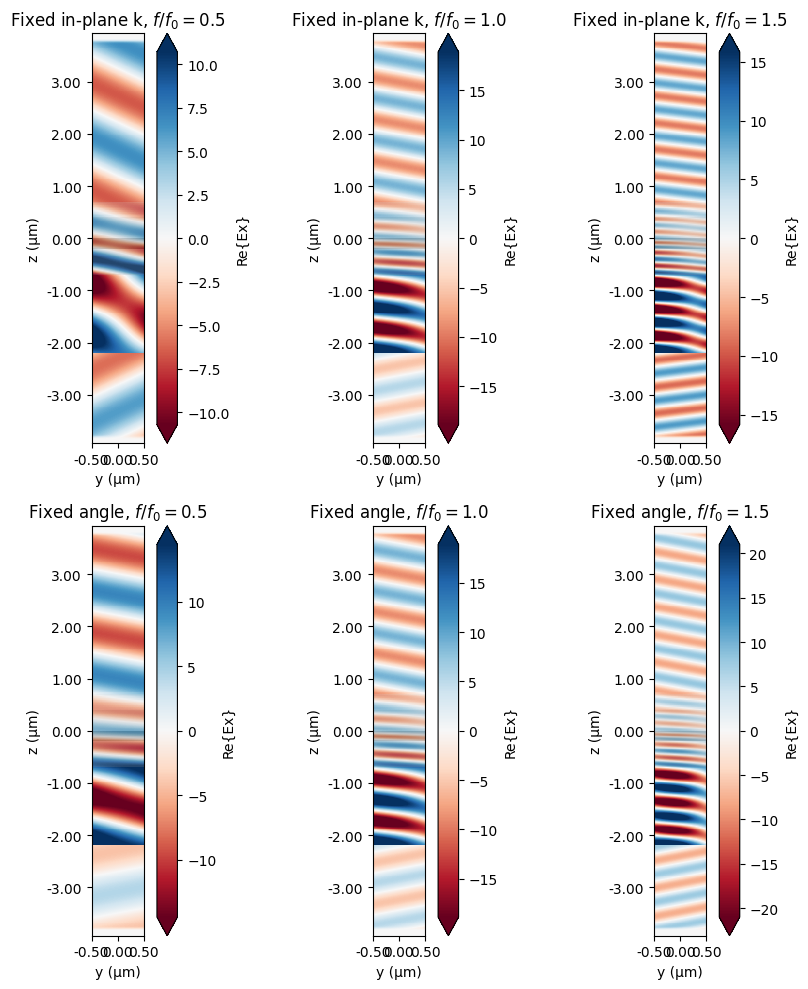
As one can see, in the fixed in-plane k case the angle of propagating plane wave changes significantly from one frequency point to another one. While in the fixed angle case the simulated plane wave propagation is performed for the same angle.

Now we perform a quantitative analysis by comparing simulation results for the transmission flux to values obtained by the Transfer Matrix Method. The code below computes expected transmission fluxes using tmm package.

These values correspond to the data record by the flux monitors. Note that for obtaining accurate results we normalize simulated transmission values by the actual injected power.

The code below plot the comparison between the TMM results and the Tidy3D simulation results.

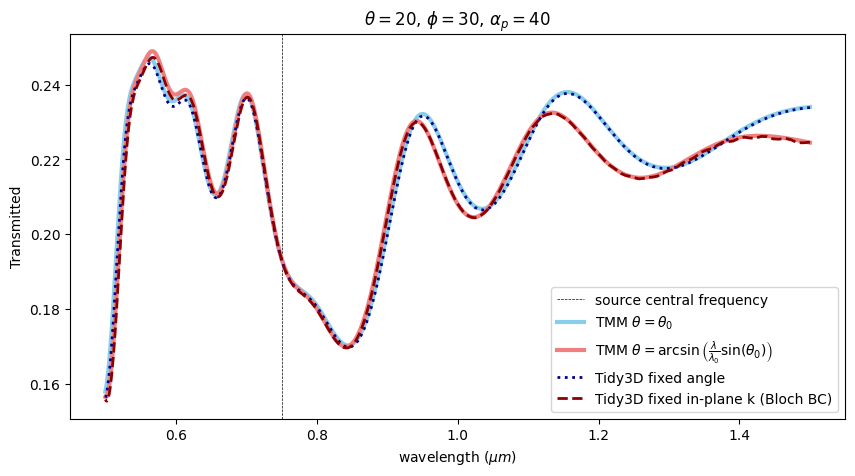
As expected the fixed in-plane k and fixed angle results coincide near the central frequency, but follow different frequency dependencies away from it.